The Harmonic Exponential Filter for Nonparametric Estimation on Motion Groups
Pre-print
Abstract. Bayesian estimation is a vital tool in robotics as it allows systems to update the belief of the robot state using incomplete information from noisy sensors. To render the state estimation problem tractable, many systems assume that the motion and measurement noise, as well as the state distribution, are all unimodal and Gaussian. However, there are numerous scenarios and systems that do not comply with these assumptions. Existing non-parametric filters that are used to model multimodal distributions have drawbacks that limit their ability to represent a diverse set of distributions. This paper introduces a novel approach to nonparametric Bayesian filtering on motion groups, designed to handle multimodal distributions using harmonic exponential distributions. This approach leverages two key insights of harmonic exponential distributions: a) the product of two distributions can be expressed as the element-wise addition of their log-likelihood Fourier coefficients, and b) the convolution of two distributions can be efficiently computed as the tensor product of their Fourier coefficients. These observations enable the development of an efficient and asymtotically exact solution to the Bayes filter up to the band limit of a Fourier transform. We demonstrate our filter's superior performance compared with established nonparametric filtering methods across a range of simulated and real-world localization tasks.
About
In this page we present an intuitive introduction to our Harmonic Exponential filter, as well as additional videos. For further information and a more detailed explanation, please refer to our paper!
Task
In this work, we address the problem of non-parametric Bayesian filtering for multimodal distributions. The goal is to estimate the posterior belief $bel(x_t) = p(x_t\vert z_{1:t},u_{1:t})$ over the state $x_t$ of an agent at time $t$, given a sequence of noisy measurements $z_{1:t}$ and controls $u_{1:t}$. We consider the case where the state space is defined on a motion group, such as $SE(2)$, with a focus on tasks involving multimodal localization from range-only and bearing-only sensors.
Method
We propose the Harmonic Exponential Filter (HEF), an exact approach to computing the posterior belief $p(x_t\vert z_{1:t},u_{1:t})$ of the Bayes filter on a compact Lie group, for band limited prior $p(x_{t-1}\vert z_{1:t-1},u_{1:t-1})$, motion $p(x_t \vert u_t, x_{t-1})$, and measurement likelihood $p(z_t \vert x_t)$. The key idea of our filter is to leverage the harmonic exponential distribution, a class of probability distributions supported on groups and homogeneous spaces and whose parameters are the Fourier coefficients of the log-likelihood function. To preserve the structure of motion groups, we use a generalized form of the Fourier transform that allows us to compute the convolution and product of two distributions efficiently. These two insights allow us to compute the prediction and update step as follows.
- Prediction step: By assuming that the motion is fully defined by the control input $u_t$, we write the motion model as the likelihood of the relative motion from $x_{t−1}$ to $x_t$, matching the relative motion induced by $u_t$. Hence, the integral $\overline{bel}(x_t) = \int_{SE(N)} p(x_t \vert u_t, x_{t-1}) bel(x_{t-1}) \, dx_{t-1}$ can be written as a convolution, which we efficiently solve using the Fourier convolution theorem.
- Update step: Given a predicted belief and measurement likelihood, both defined with the density of the harmonic exponential distribution, the update step is computed via an element-wise addition of the parameters of the two densities.
- Normalization: We can compute the normalization constant using Fourier analysis and retrieve the posterior belief.
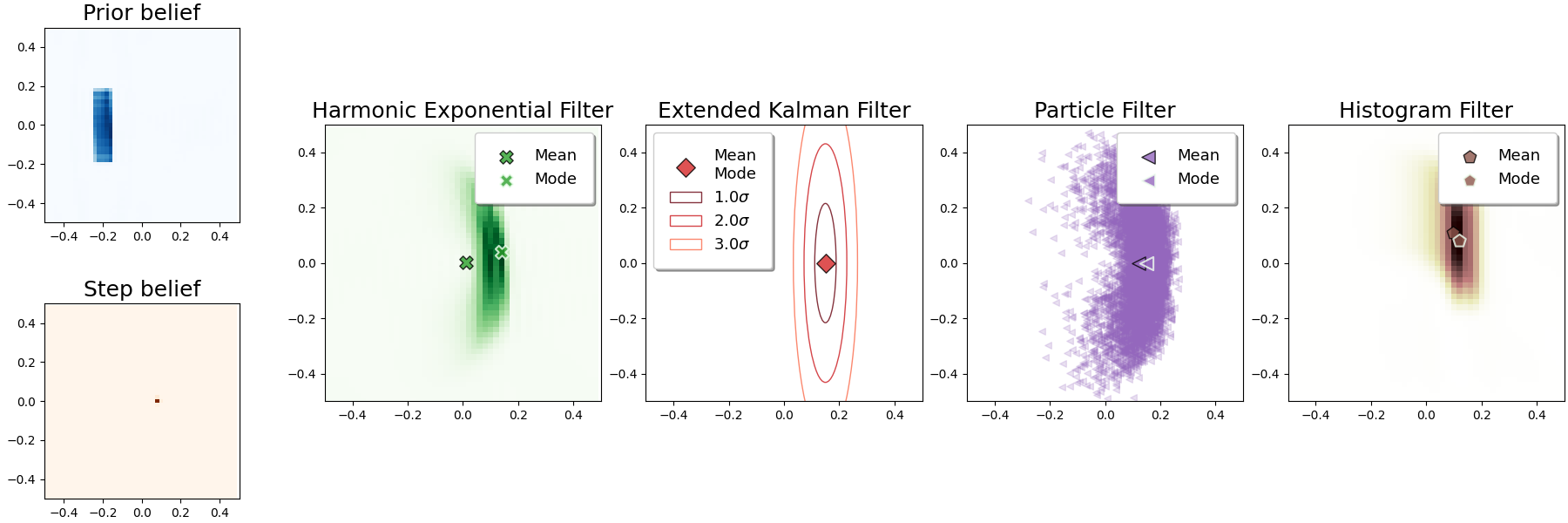
To showcase the effectiveness of our approach capturing real-world distributions, we model the banana-shape distribution with our filter. This distribution appears when the uncertainty in the heading of an agent increases due to the accumulation of error during multiple prediction steps. Starting from a rectangular prior and a Gaussian motion likelihood, we take steps in a horizontal straight path to the right. As expected, the banana-shape distribution emerges after few iterations.
We compare the ability of our HEF capturing the banana-shape distribution against four other well established filtering approaches in the literature. The results highlight how only the HEF, IEKF and particle filter are capable of modeling it.
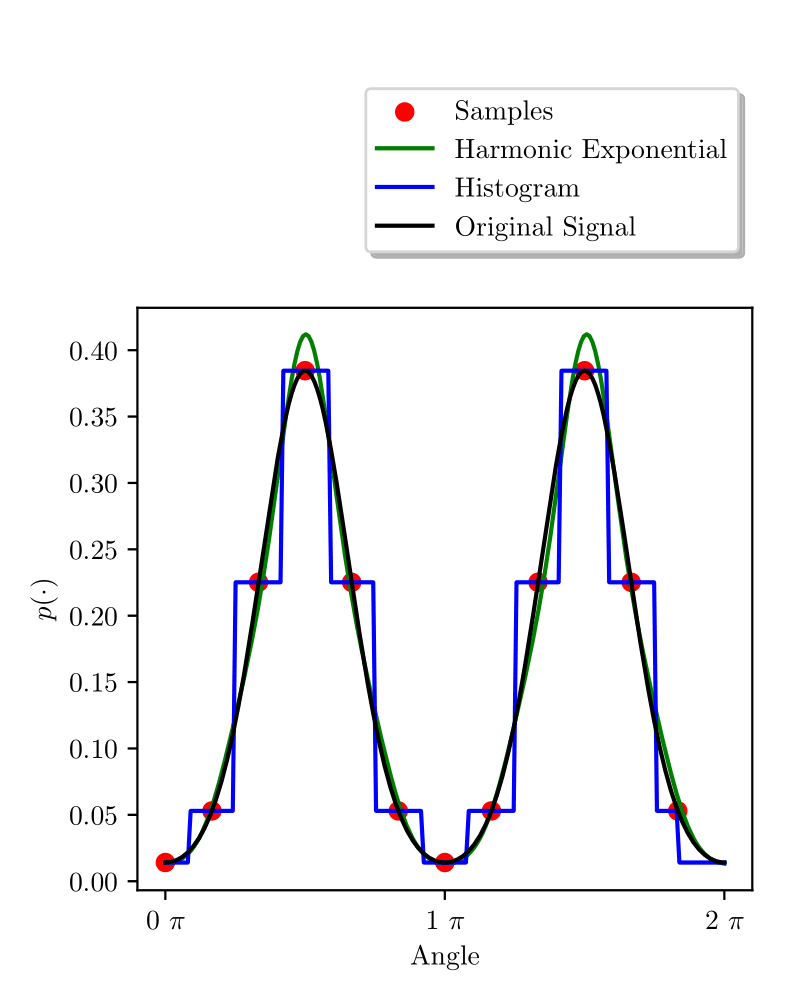
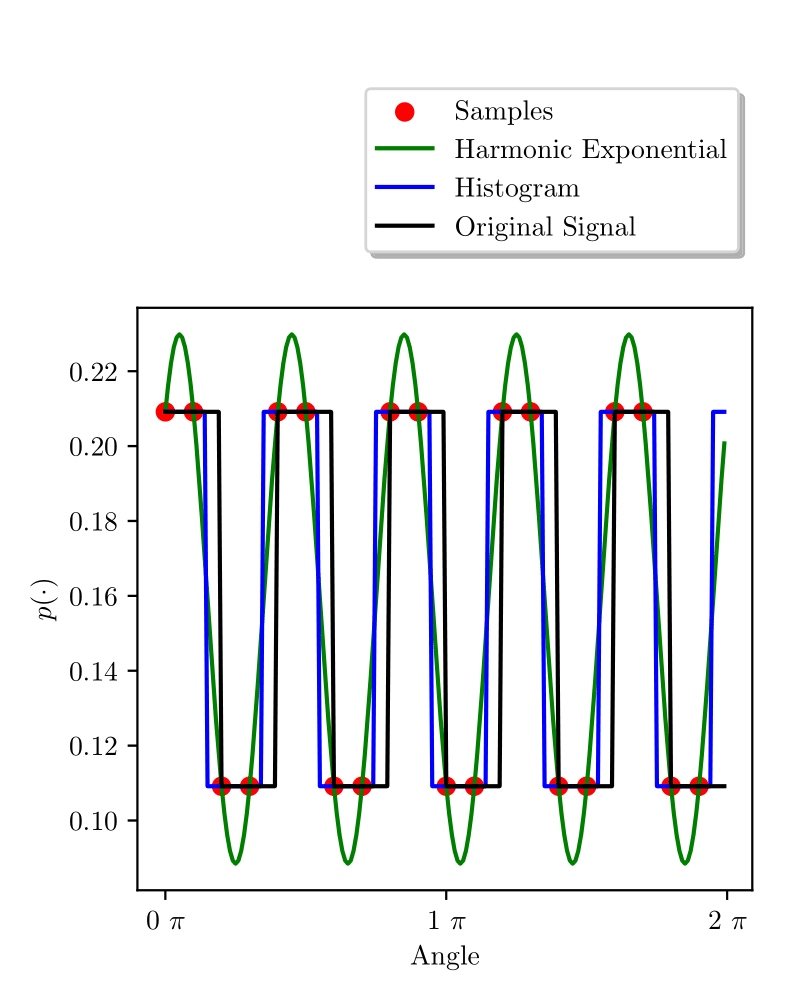
We demonstrate how the HEF effectively models both continuous and discrete densities, comparing it to a histogram-based approach. While the histogram excels at capturing square-like distributions, the HEF performs better at modeling continuous densities, as evidenced by a lower Kullback–Leibler divergence. As motion and measurement models are typically smoothly-varying functions, the HEF is a good candidate for many real-world robotics applications.
Lastly, we present a runtime comparison between a histogram-based approach and the HEF for computing the convolution of two functions. Hist (PP) is a direct convolution written in pure python. Hist (Scipy) uses the $\texttt{scipy.signal.convolve()}$ function, and the HEF, implemented in python using the Numpy FFT library.
The results show how the histogram approach quickly becomes intractable while ours scale more gracefully.
Experimental setup
All our experiments focus on two main metrics. The first metric is the absolute trajectory error (ATE), calculated using two different estimators of the robot position: the mode and the mean of the posterior belief. The ATE, measured in meters, is calculated along the entire trajectory, and we also report its standard deviation. However, as this metric does not entirely encapsulate the non-Gaussian nature of these estimators, we also calculate the negative log-posterior (NLP) of the ground truth position under the current belief. In these assessments, our proposed HEF is compared against the following filtering approaches: an EKF implementation that assumes unimodal Gaussian state and error, a histogram filter (HistF), and a particle filter (PF).
Simulation experiments
The simulation experiments use range-only measurements. This environment includes a series of landmarks arranged in a line. The robot travels in a counterclockwise circle around the landmarks. The landmarks alternate in providing a range measurement at each timestamp, where we assume known correspondence. All experiments but the EKF start from a bi-modal prior.
We showcase the performance of HEF in this localization task and show the predicted belief, $\overline{bel}(x_t)$, measurement likelihood, $p(z_t \vert x_t)$, and posterior belief, $bel(x_t)$, at each timestamp alongside its posterior mean estimate (left). Similarly, we show the uncertainty of the HEF and the baselines (right).
The quantitative results of this experiment are presented in the following table, where metrics are computed over 10 different random seeds. Overall, our filter is comparable if not better than the baselines.
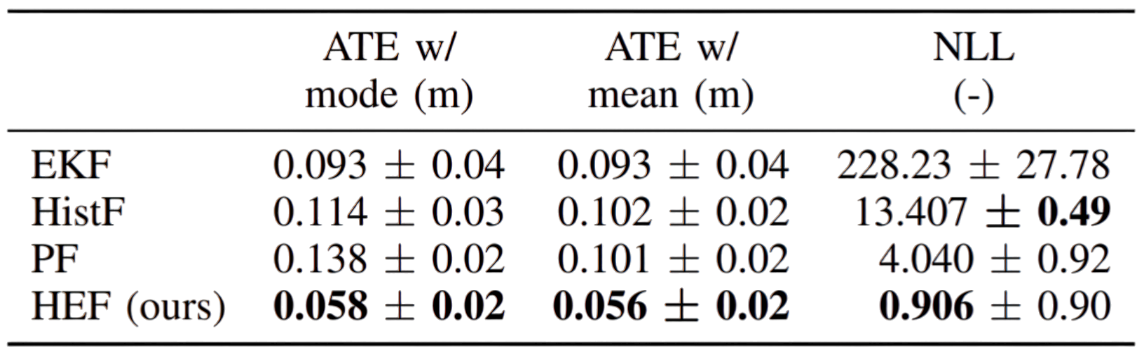
UWB experiments
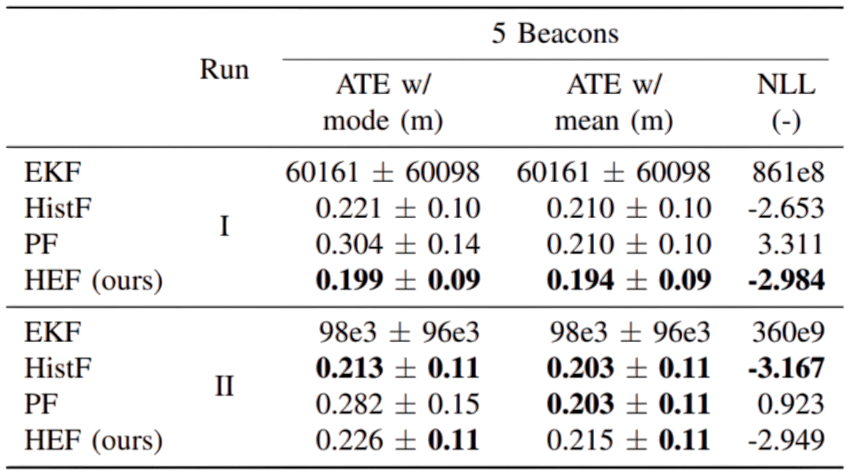
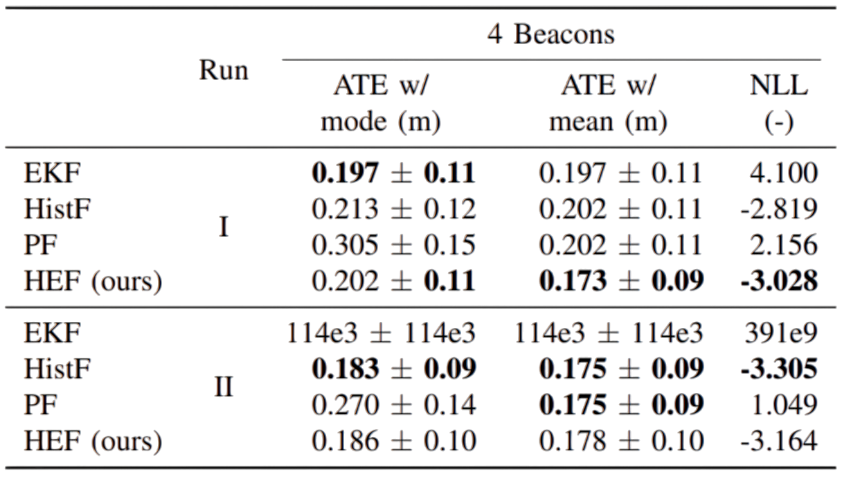
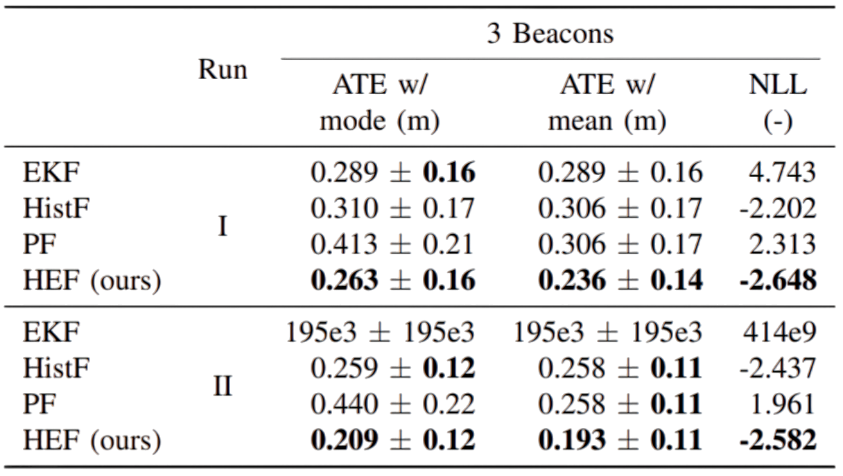
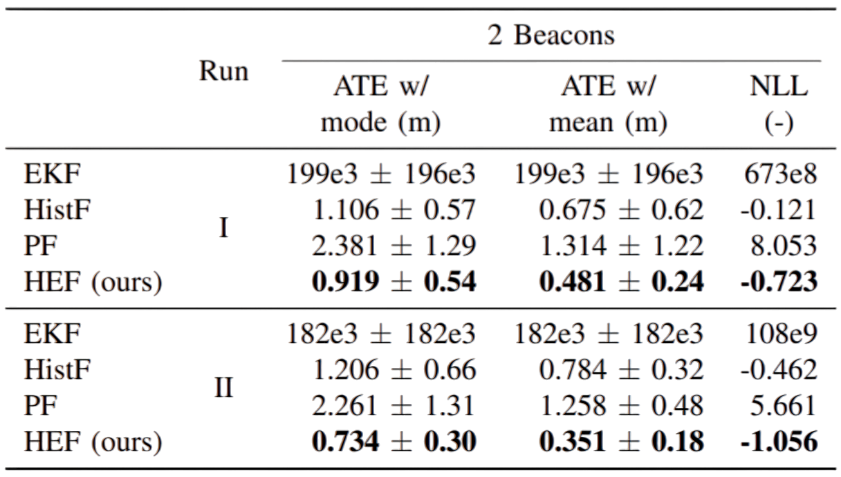
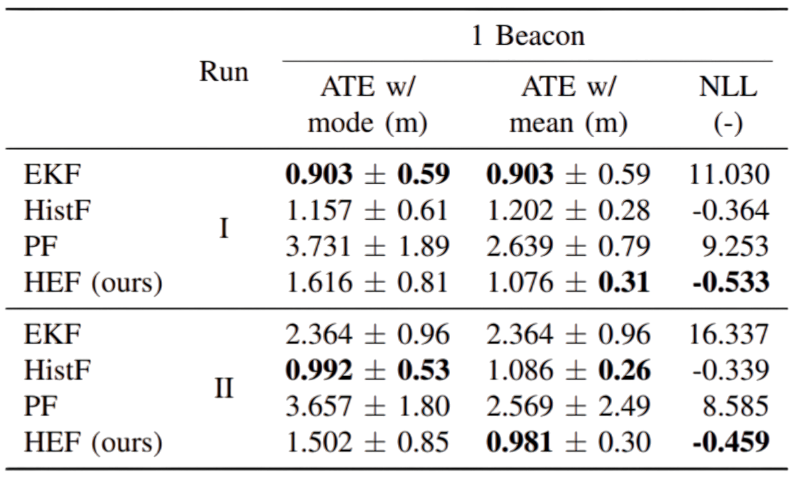
For the UWB experiments, we used a Clearpath Husky unmanned ground vehicle (UGV). The UGV is equipped with an ultra-wideband (UWB) tag that communicates with stationary UWB beacons in the surrounding room. Using a ranging protocol between the UGV-mounted UWB tag and the stationary UWB beacons, range measurements between each are computed. The experiment consists of two runs, each with a total of five beacons that were premapped prior to the experiment. For each run, we removed beacons one by one by ignoring their range measurements, producing a total of five trials per run. We assume known correspondence. The motion of the robot is estimated from noisy odometry and IMU data.
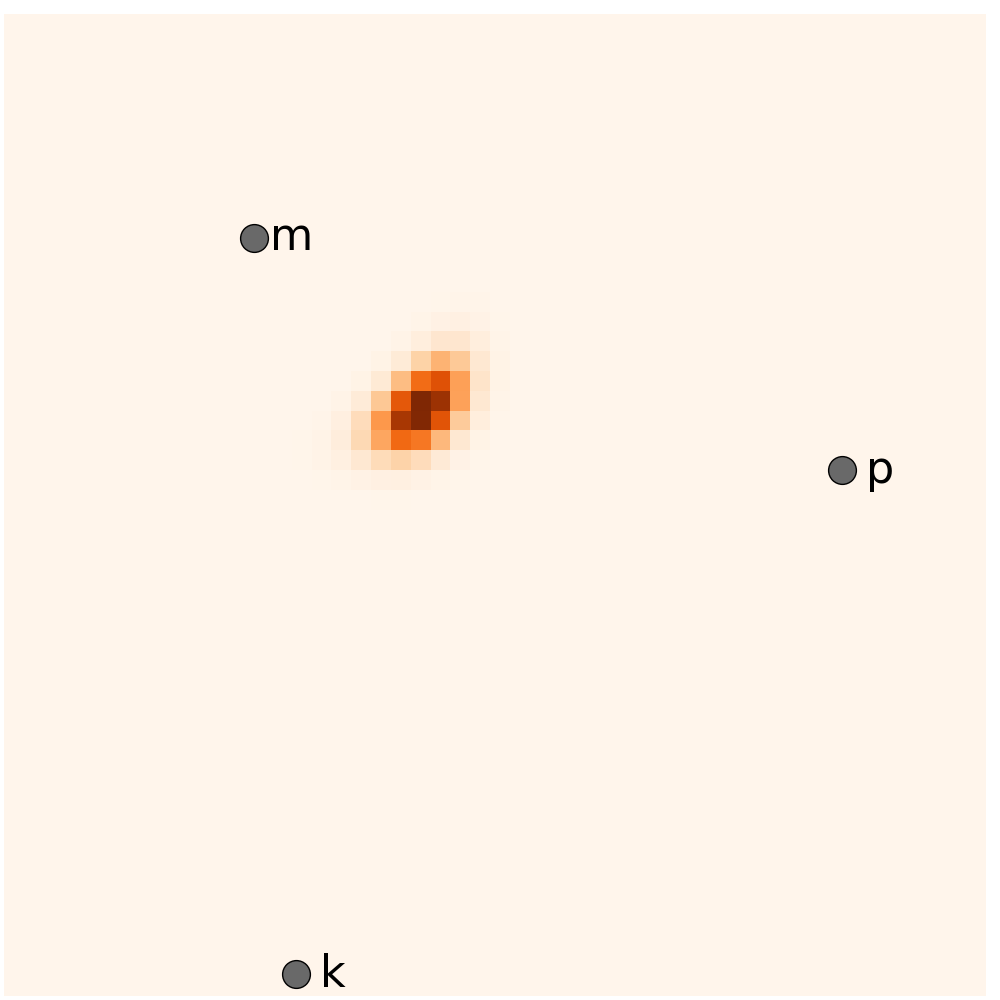
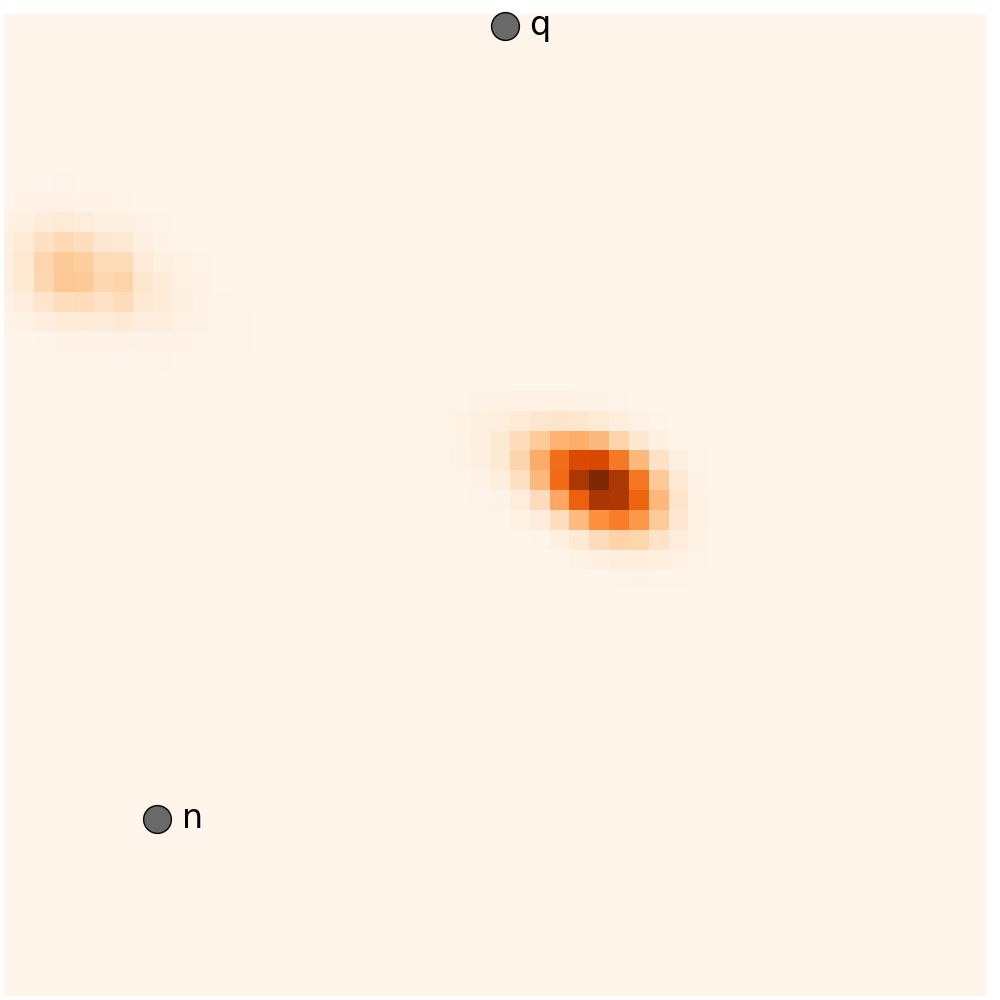
We present the performance of the HEF and the baselines during the two runs, with different landmark configurations. The left column are from the first run and the right one from the second run.
Run 1 - Five landmarks
Run 2 - Five landmarks
Run 1 - Four landmarks
Run 2 - Four landmarks
Run 1 - Three landmarks
Run 2 - Three landmarks
Run 1 - Two landmarks
Run 2 - Two landmarks
Run 1 - One landmarks
Run 2 - One landmarks
The quantitative evaluation in this real-world experiments highlights the performance of our filter.
Doors’ experiments
This experiment consists of localizing an agent navigating in an anticlockwise direction in a corridor using doors detected in RGB images as landmarks. All doors share similar semantic features, such as color or handle. Therefore, we do not assume known correspondence on which of the 21 doors generated a given measurement. We premapped the environment using gmapping and assumed a bearing-only measurement model. Bearing measurements are computed using the centroid of the doors. We integrate the IMU and wheel encoders to estimate the motion of a Jackal platform.
The quantitative results of this experiments are presented below.
Citation
@article{saavedra2024hef,
title = {The Harmonic Exponential Filter for Nonparametric Estimation on Motion Groups},
author = {Saavedra-Ruiz Miguel, Parkison Steven, Arora Ria, Forbes James, and Paull Liam},
journal = {arXiv preprint arXiv:2408.00907},
year = {2024}
}
|
|
