One-4-All: Neural Potential Fields for Embodied Navigation
IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2023)
Abstract. A fundamental task in robotics is to navigate between two locations. In particular, real-world navigation can require long-horizon planning using high-dimensional RGB images, which poses a substantial challenge for end-to-end learning-based approaches. Current semi-parametric methods instead achieve long-horizon navigation by combining learned modules with a topological memory of the environment, often represented as a graph over previously collected images. However, using these graphs in practice requires tuning a number of pruning heuristics. These heuristics are necessary to avoid spurious edges, limit runtime memory usage and maintain reasonably fast graph queries in large environments. In this work, we present One-4-All (O4A), a method leveraging self-supervised and manifold learning to obtain a graph-free, end-to-end navigation pipeline in which the goal is specified as an image. Navigation is achieved by greedily minimizing a potential function defined continuously over image embeddings. Our system is trained offline on non-expert exploration sequences of RGB data and controls, and does not require any depth or pose measurements. We show that O4A can reach long-range goals in 8 simulated Gibson indoor environments and that resulting embeddings are topologically similar to ground truth maps, even if no pose is observed. We further demonstrate successful real-world navigation using a Jackal UGV platform.
About
This page aims to present an overview of our method, as well as additional videos, figures and experiment details. Have a look at our paper and at our IROS video for an in-depth presentation of the method!
Task
We consider a robot with a discrete action space $\actions = \{\mathtt{STOP}, \mathtt{FORWARD}, \mathtt{ROTATE\_ RIGHT}, \mathtt{ROTATE\_ LEFT}\}$ for an image-goal navigation task. Using our knowledge of the robot's geometry and an appropriate exteroceptive onboard sensor (e.g., a front laser scanner), we assume that the set of collision-free actions $\freeactions$ can be estimated. When prompted with a goal image, the agent should navigate to the goal location in a partially observable setting using only RGB observations $\obs_t$ and the $\freeactions$ estimates. The agent further needs to identify when the goal has been reached by autonomously calling the $\mathtt{STOP}$ action in the vicinity of the goal.
Method
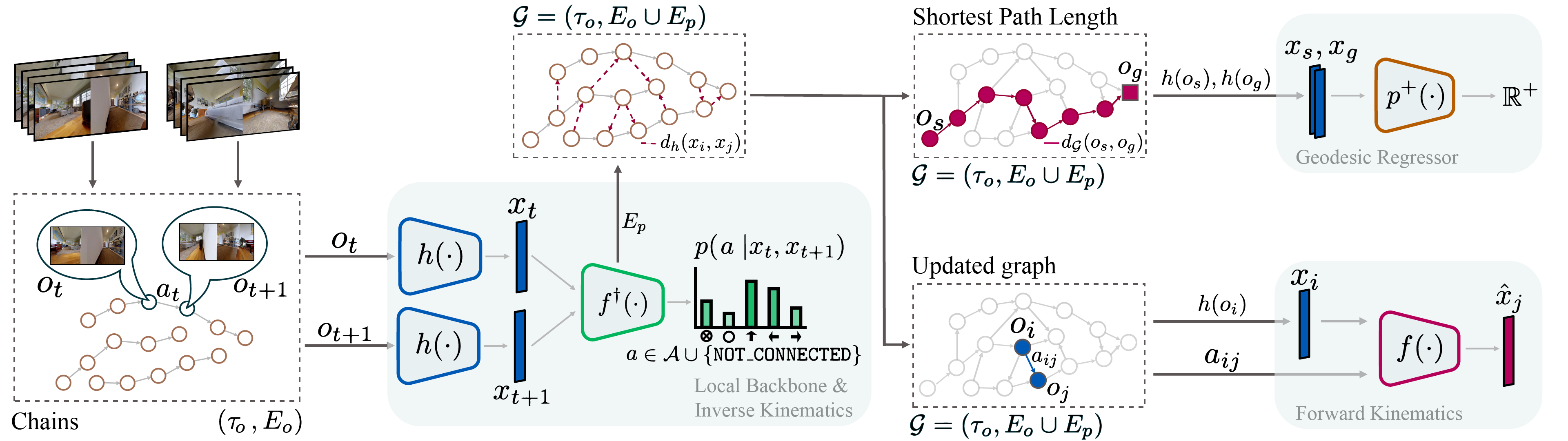
O4A consists of 4 learnable deep networks trained with previously collected RGB observation trajectories $\tau_{\obs} =\{\obs_t\}_{t=1}^T$ and corresponding actions $\actiontraj = \{a_t\}_{t=1}^T$, without pose:
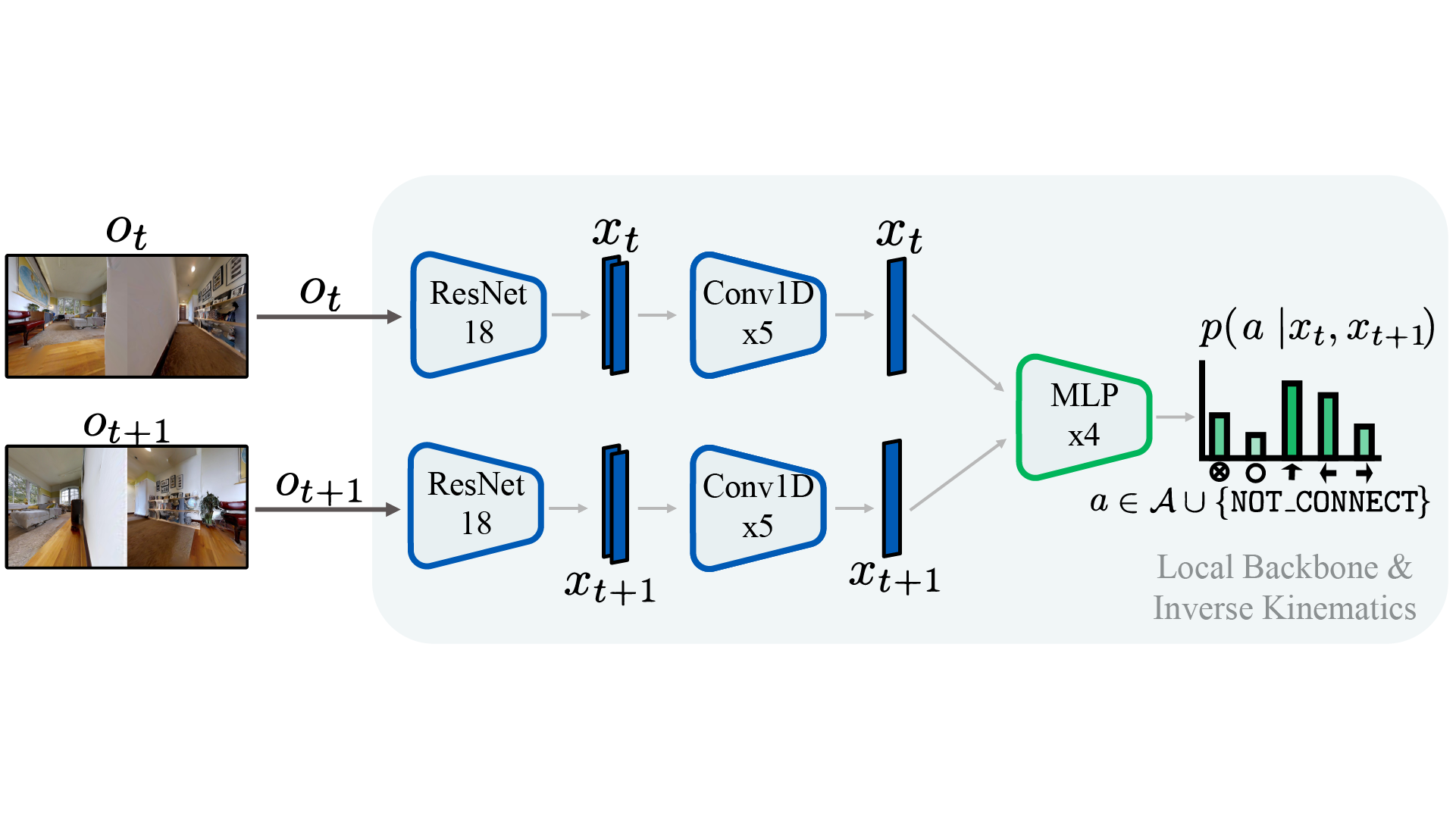
- The local backbone $\local$ (left) takes as input RGB images to produce low-dimensional latent embeddings $\code \in \latentspace$ and is trained with a self-supervised time contrastive objective. Once trained, the local backbone can output a local metric $\norm{\code_t - \code_s}$ to measure similarity between observations. The extracted embeddings will also be used as inputs for other modules;
- The inverse kinematics head $\conn$ (center) uses pairs of embeddings to predict the action required to traverse from one embedding to the other (order matters), or the inability to do so through the $\mathtt{NOT\_CONNECTED}$ output;
$\local$ and $\conn$ can then perform loop closures over $\tau_{\obs}$ and construct a directed graph $\graph$, where nodes represent images. Edges represent one-action traversability and are weighted using the local metric. $\graph$ will not be required for navigation, and is only relied on to derive training objectives for the last two components:
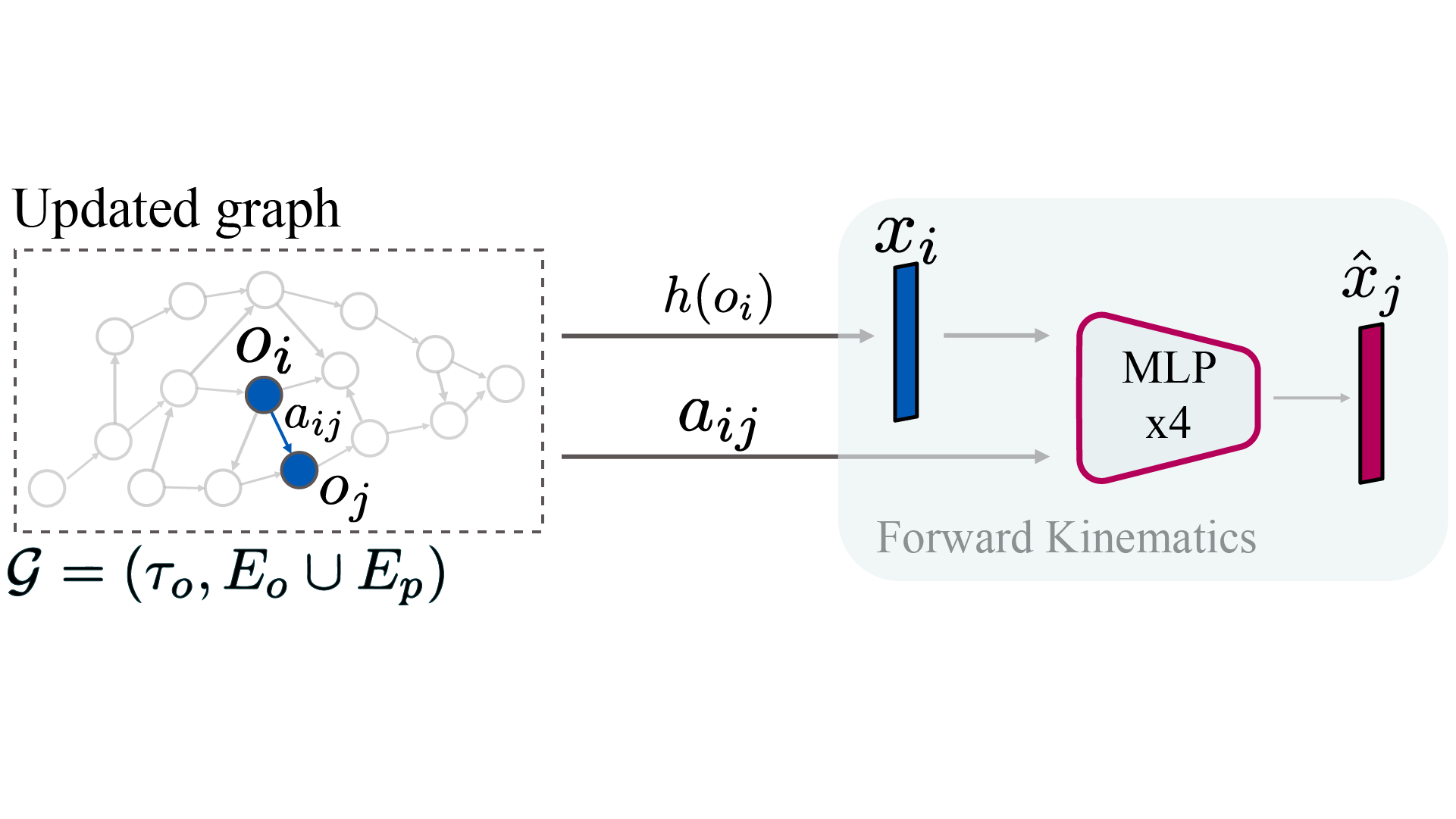
- The forward kinematics head (bottom right) $\fd$ is trained using edges from $\graph$ to predict the next embedding $\code_j$ given the current embedding $\code_i$ and an action $a_{ij} \in \actions$;
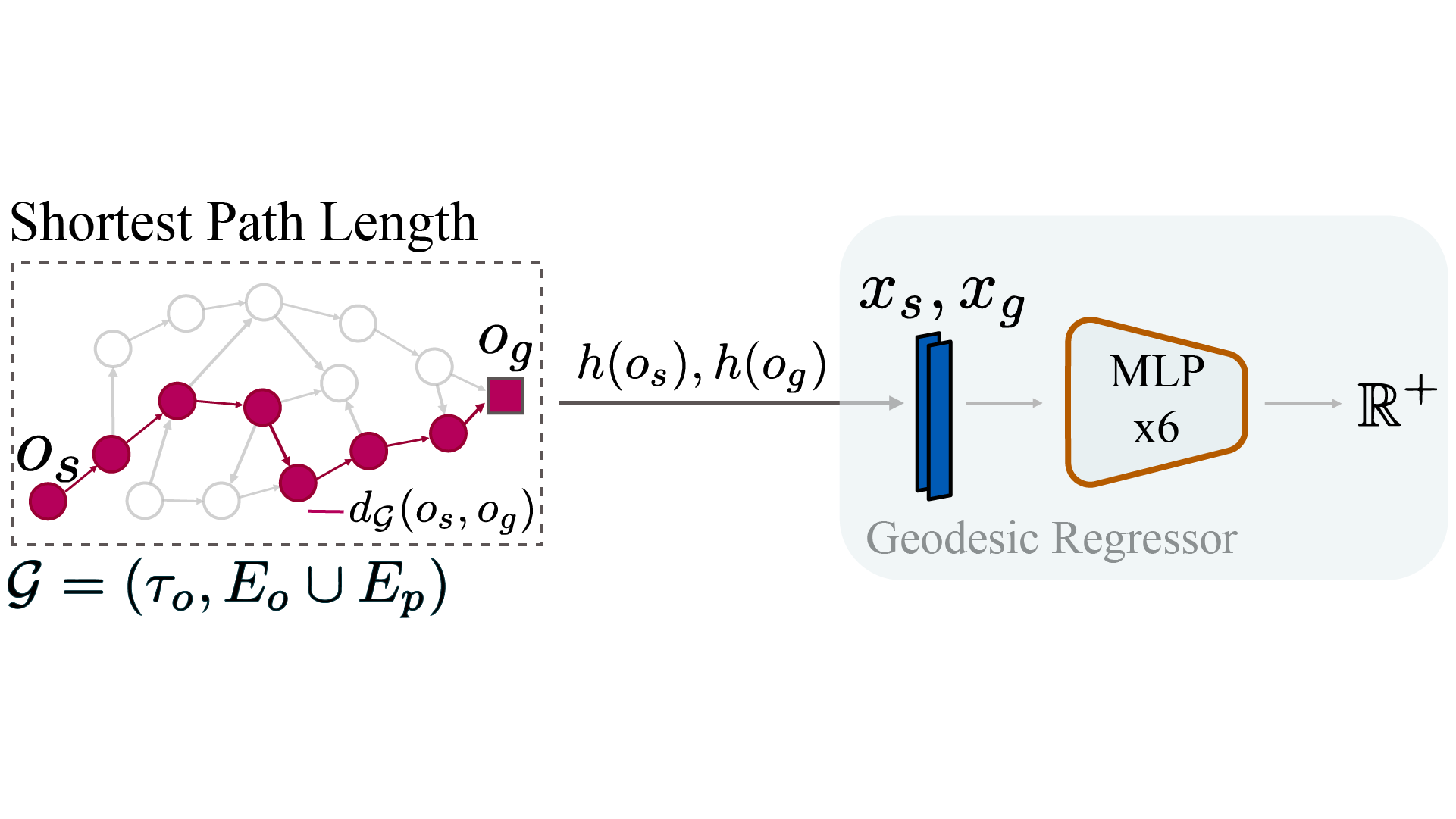
- The geodesic regressor $\georeg$ (top right), which learns to predict the shortest path length between images embeddings. $\georeg$ is the core planning module and can be interpreted as encoding the geometry of $\graph$.
When multiple environments are considered, $\local$, $\conn$ and $\fd$ are shared across environments, and we train environment-specific regressors $\georeg_i$.
Navigation
The geodesic regressor $\georeg$ provides a powerful signal to navigate to a goal image (green goal marker). Indeed, it factors in the environment geometry and can, for example, drive an agent out of a dead end to reach a goal that is close in terms of Euclidean distance, but far geodesically. We use $\georeg$ as the attractor in a potential function $\mathcal{P}$ in tandem with repulsors $p^{-}$ around previously visited observations (red markers). At each step, the agent picks the action that leads to a potential-minimizing waypoint W. While we illustrate the potential function on the map, it is in fact defined directly over image embeddings in $\latentspace$.

Furthermore, we call $\mathtt{STOP}$ by thresholding the local metric between the current image and the goal image. We found this to be more reliable than relying on $\conn$.
Simulation Experiments
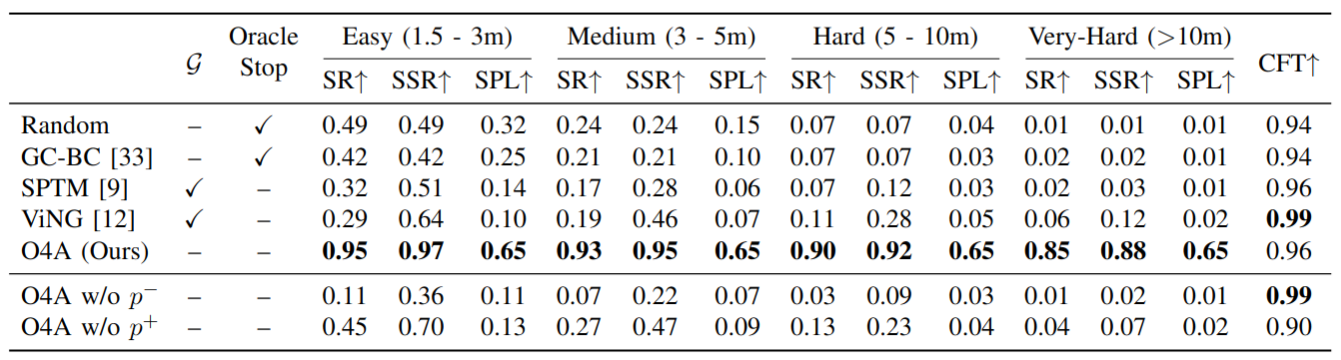
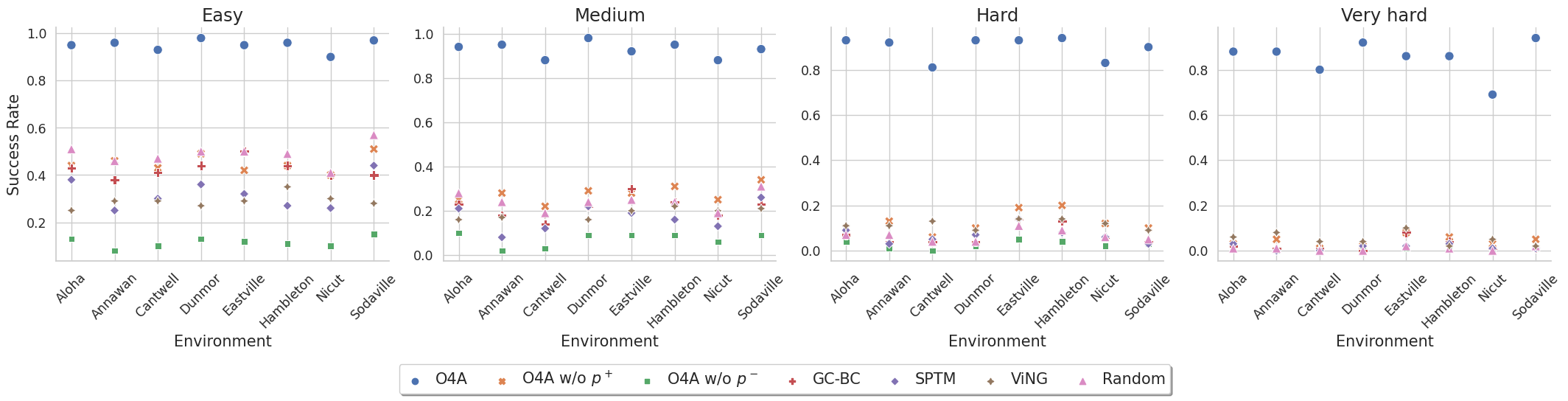
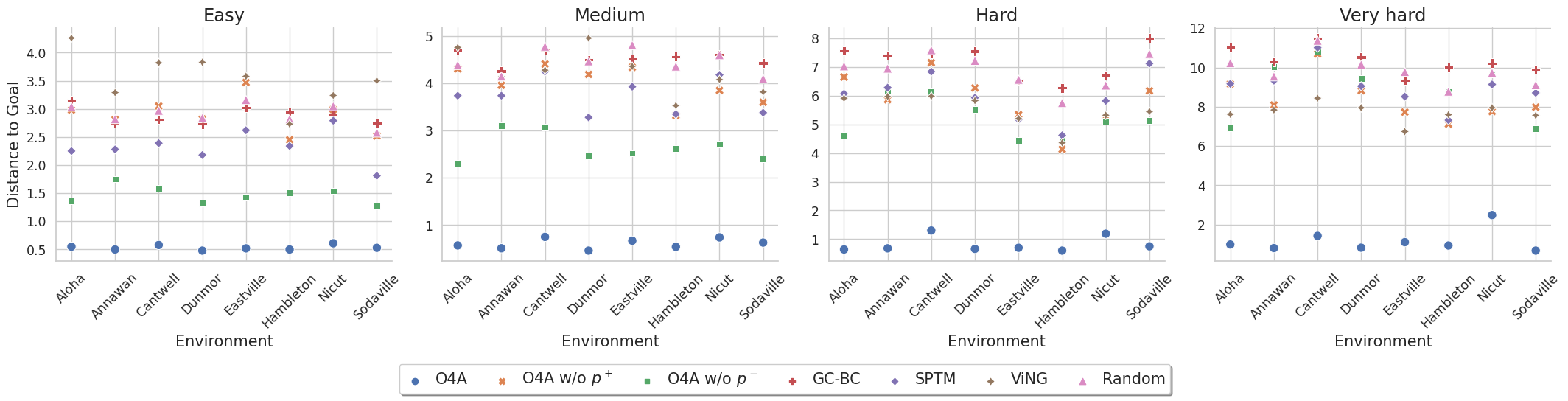
We perform our simulation experiments using 8 scenes from the Gibson dataset rendered with the Habitat simulator. Trajectories are categorized into easy (1.5 $-$ 3m), medium (3 $-$ 5m), hard (5 $-$ 10m) and very hard (> 10m) based on their geodesic distance to the goal. The agent is a differential drive robot with two RGB cameras, one facing forward and the other facing backward. We showcase O4A trajectories for all scenes (rows) and difficulty levels (columns).
Aloha
Annawan
Cantwell
Dunmor
Eastville
Hambleton
Nicut
Sodaville
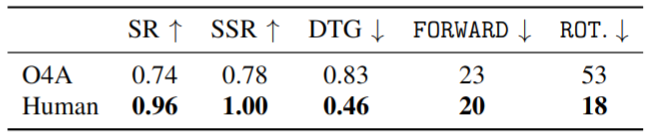
Robot Experiments
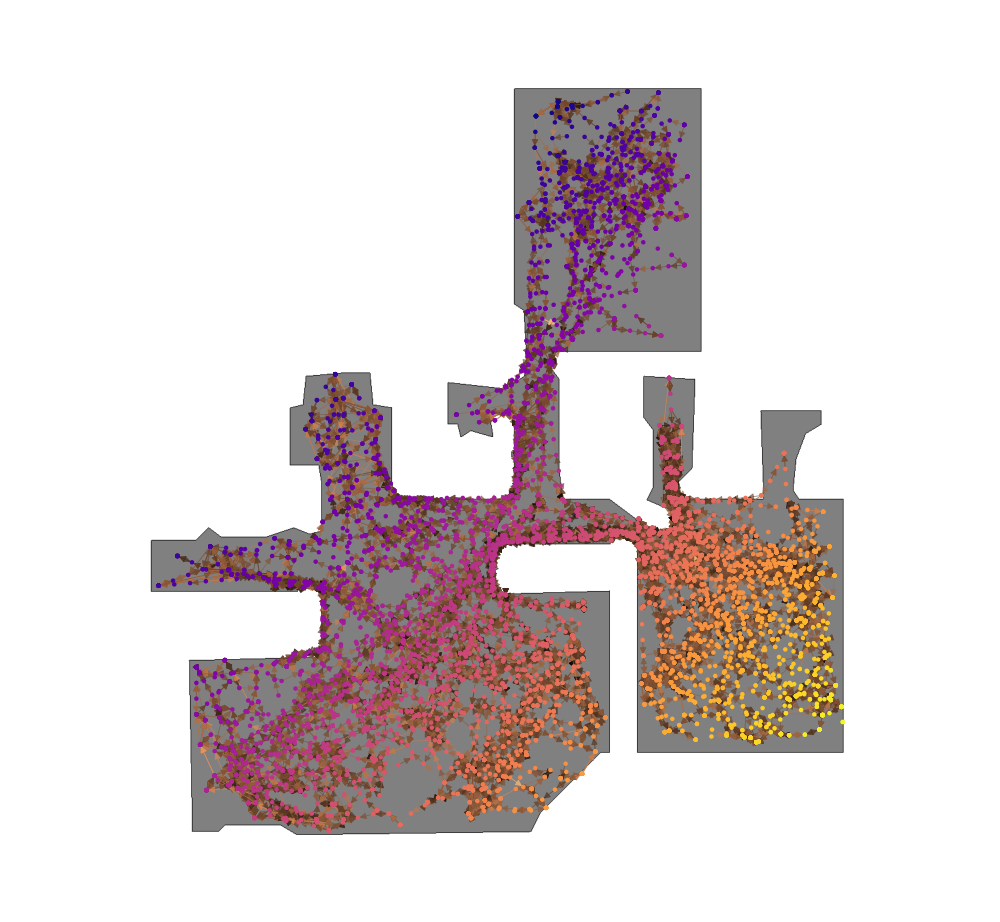
Embeddings


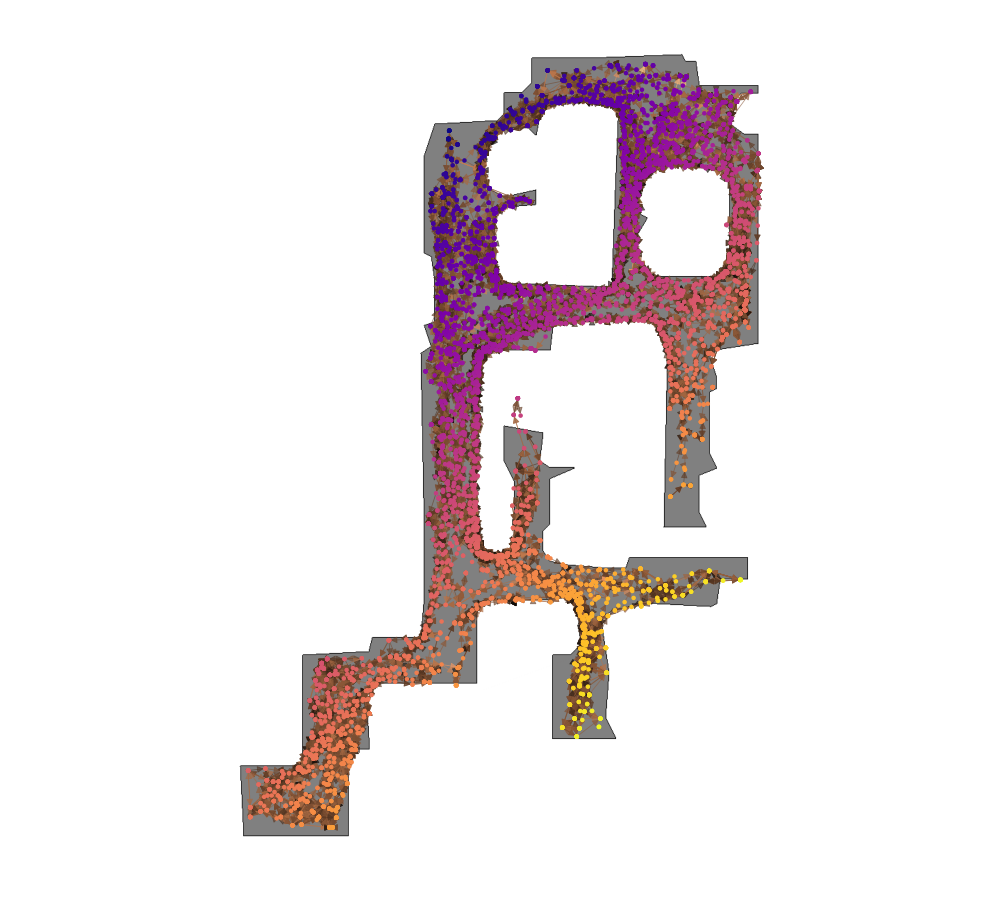
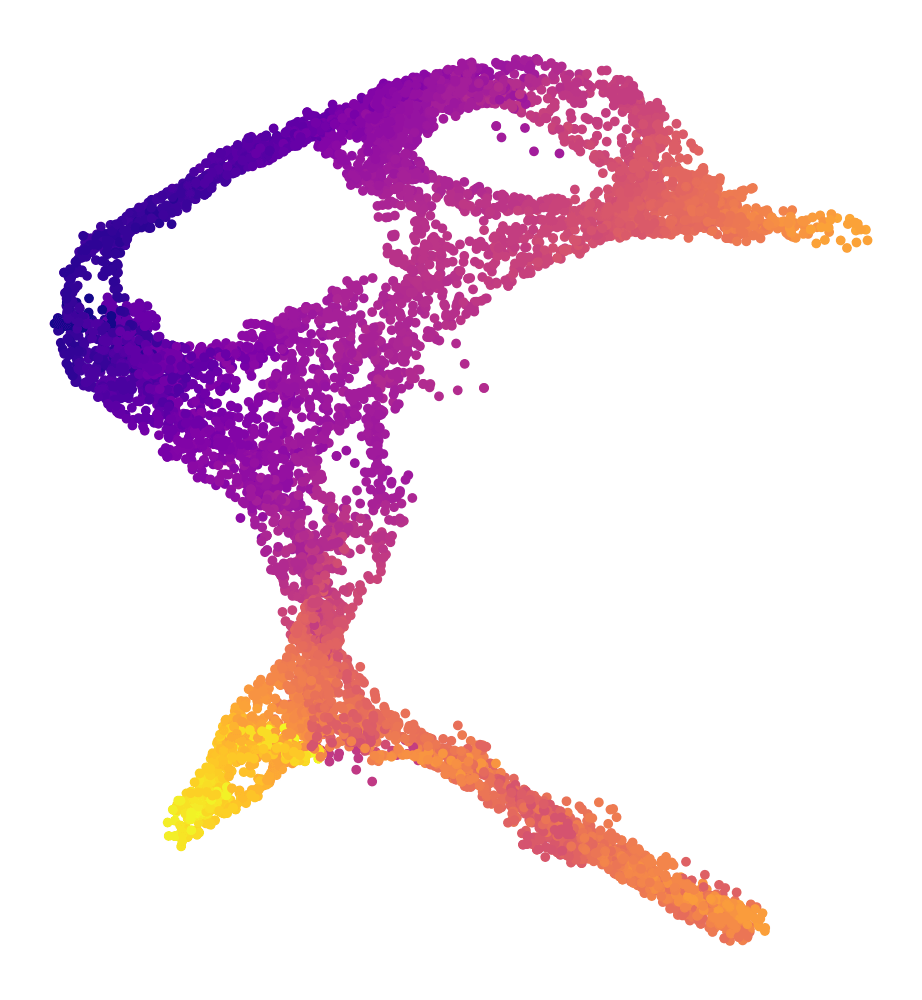

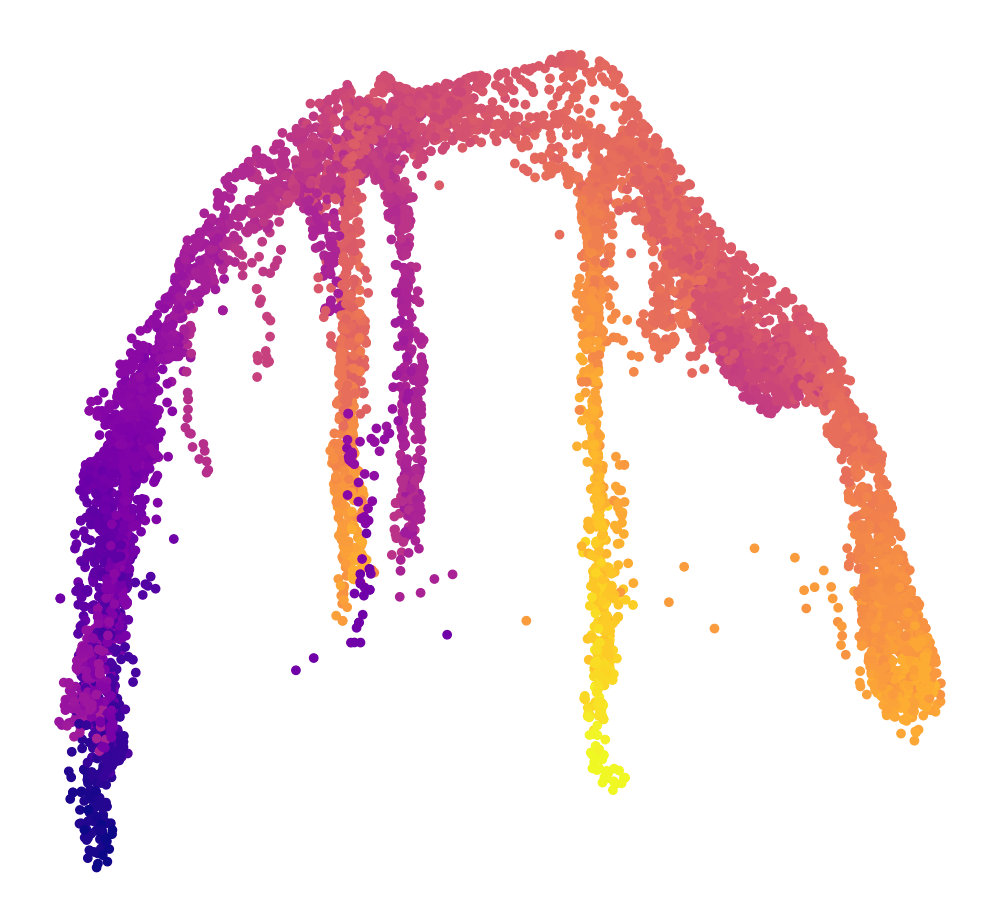
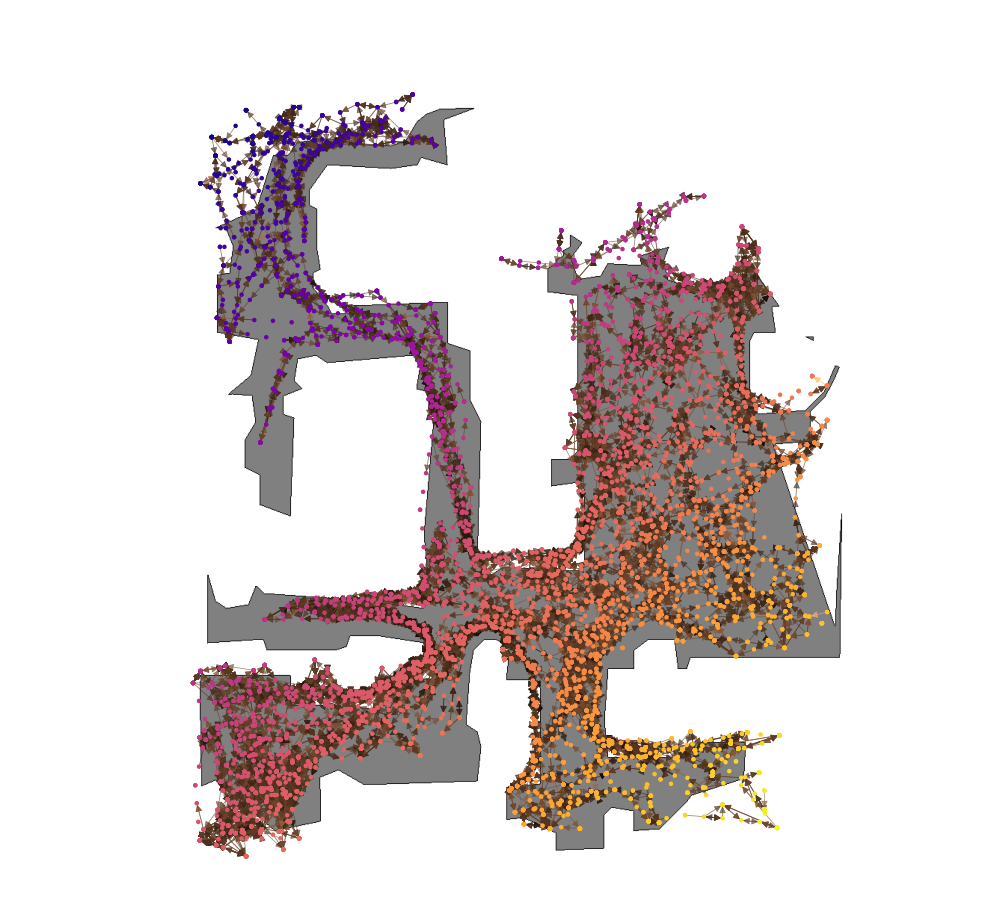
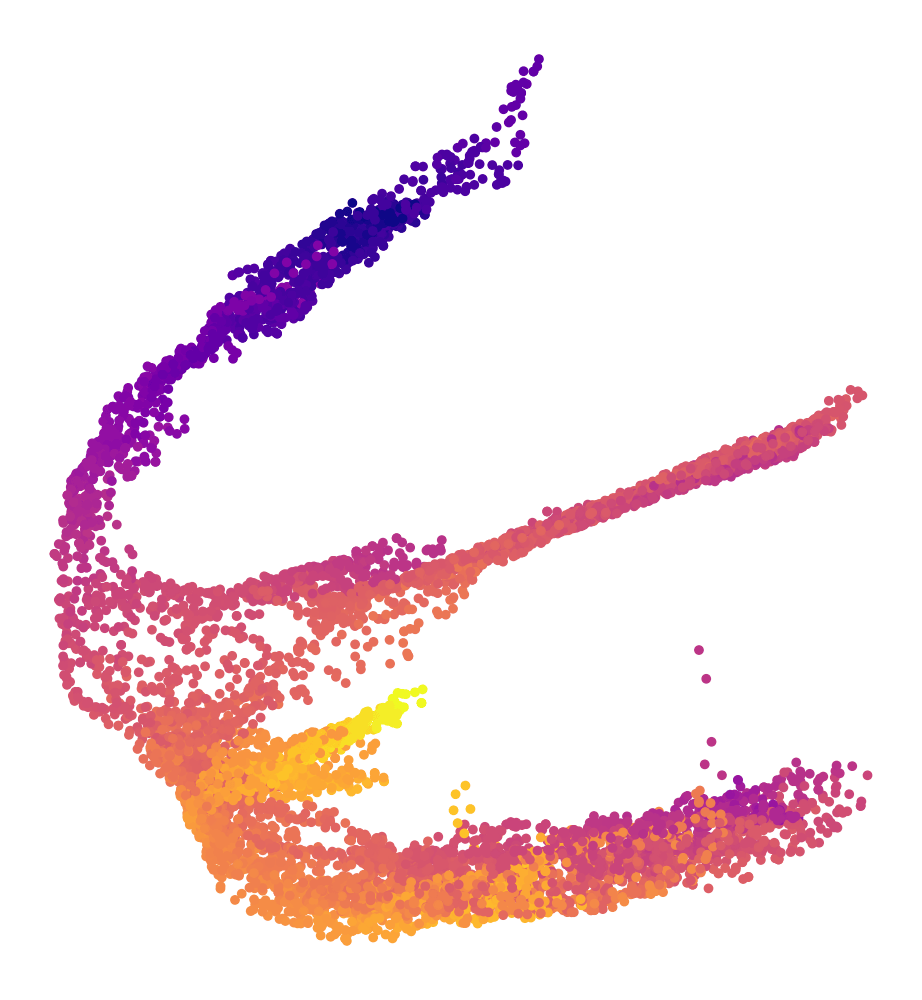






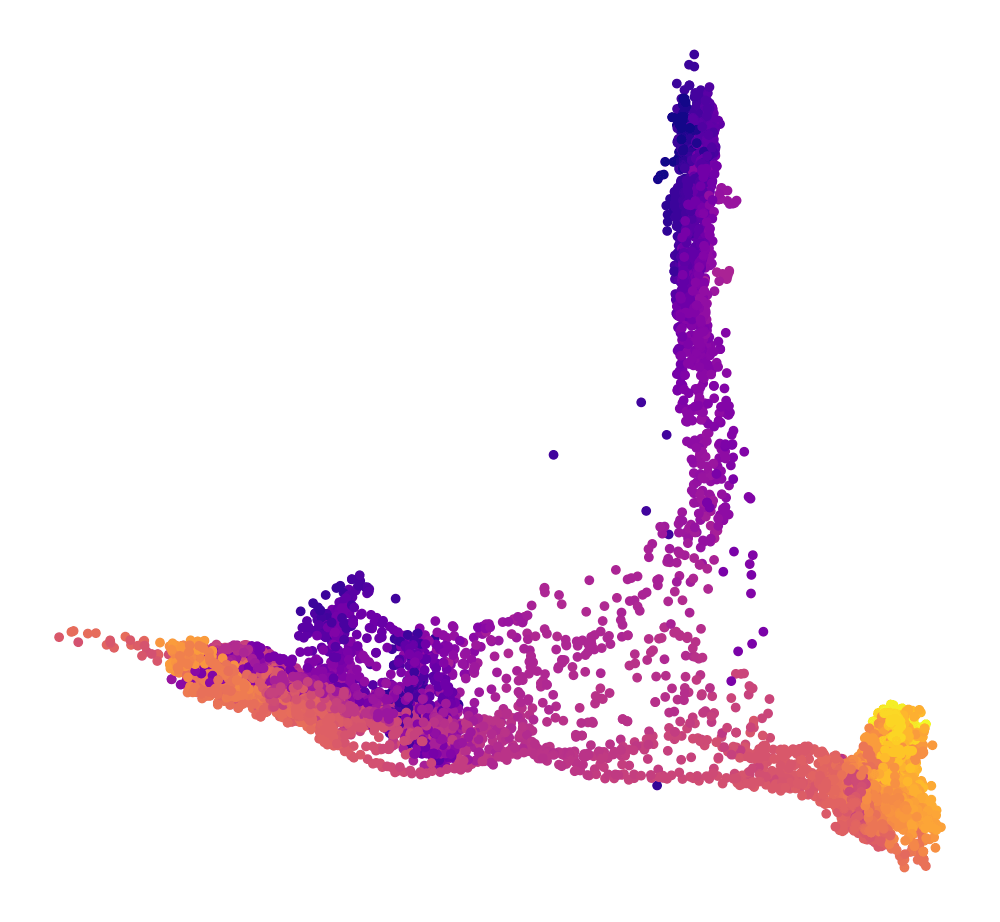
Detailed architectures and baselines
We finally show detailed architectures and hyperparameters for O4A and the baselines we used.
O4A
SPTM
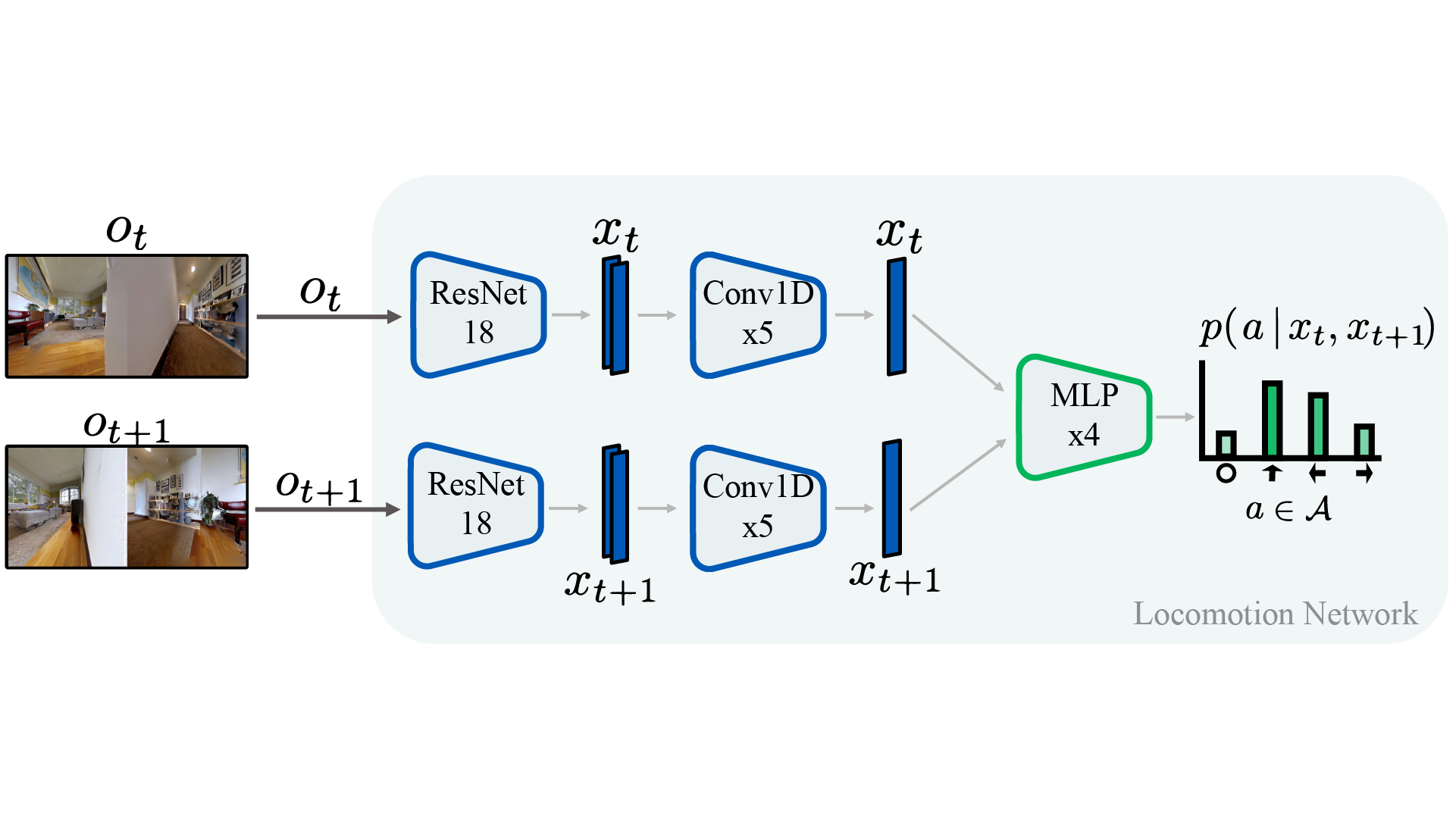
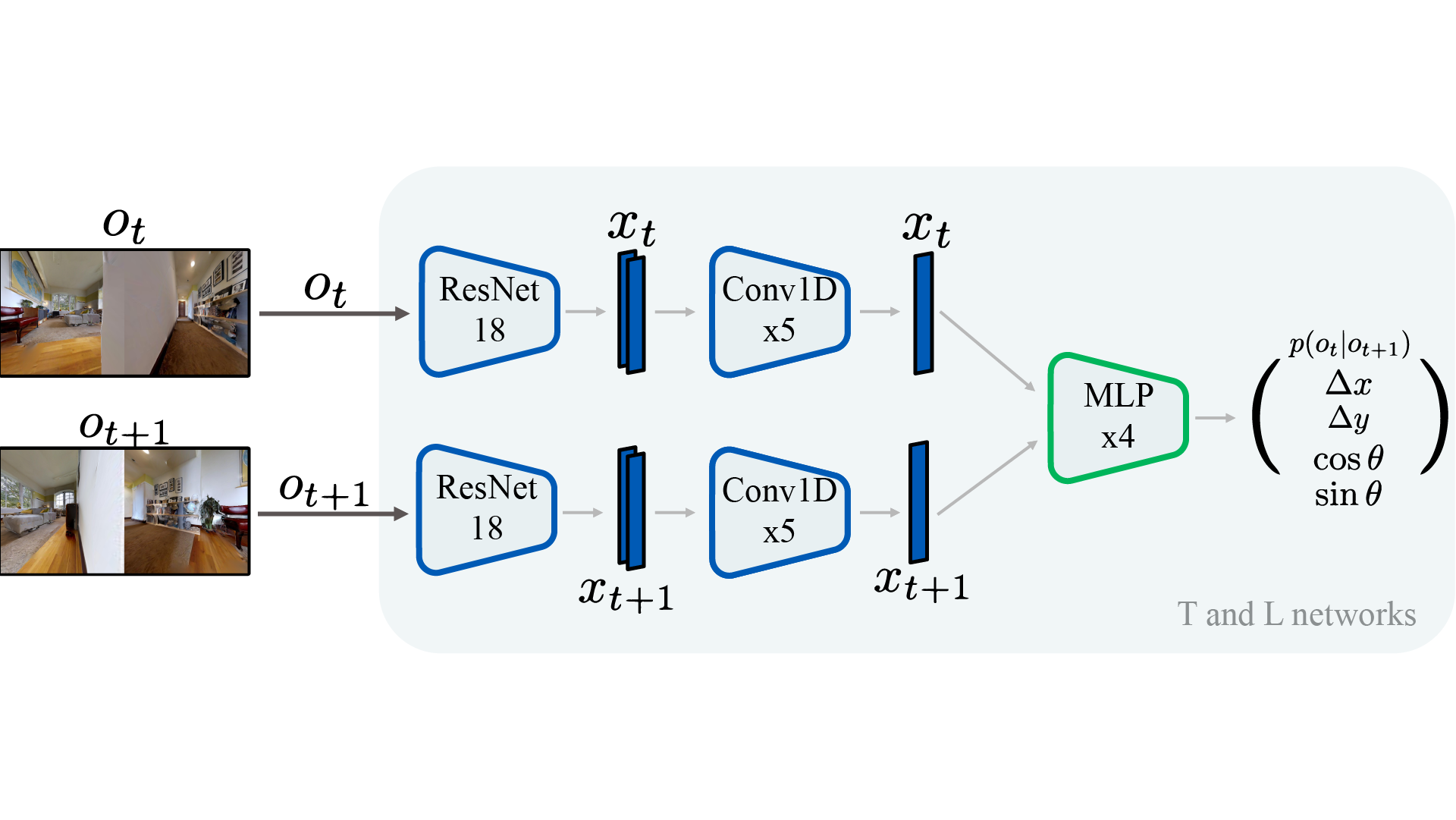
ViNG
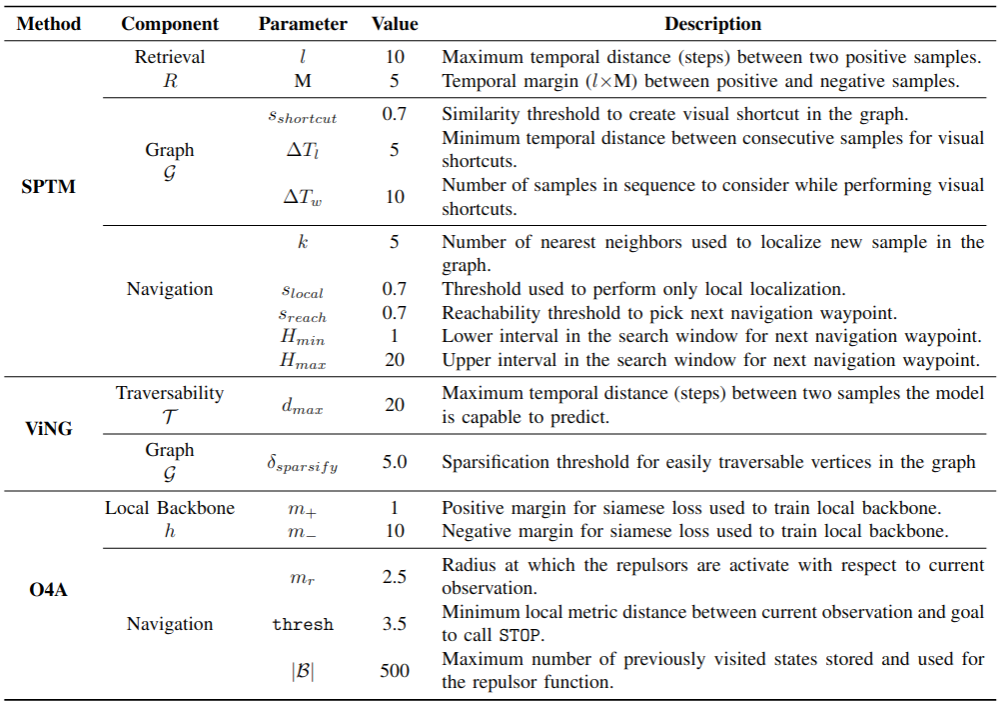
Hyperparameters
Extra plots for the Simulation Experiments
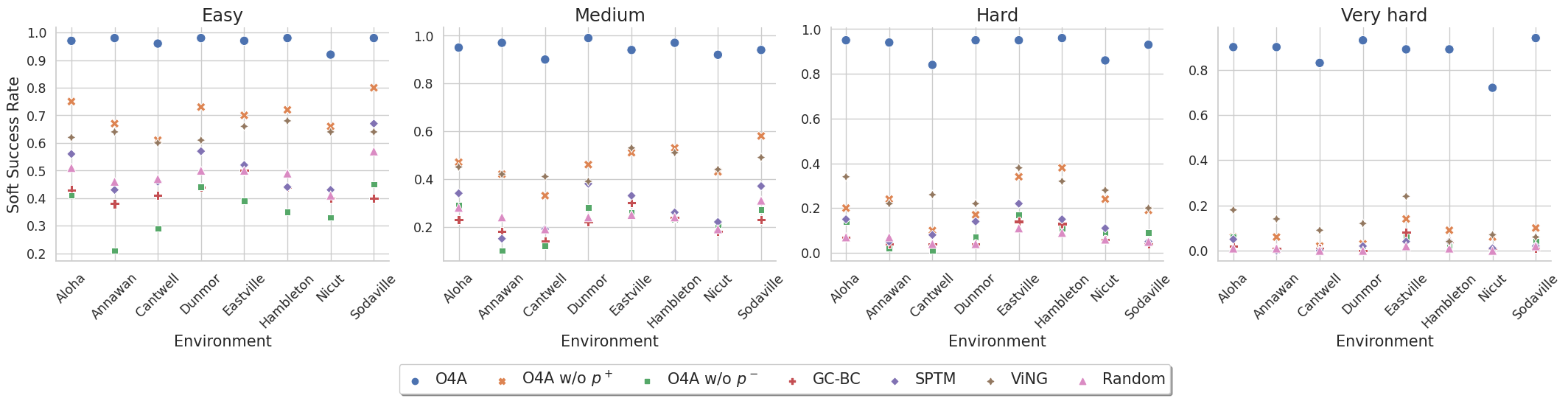
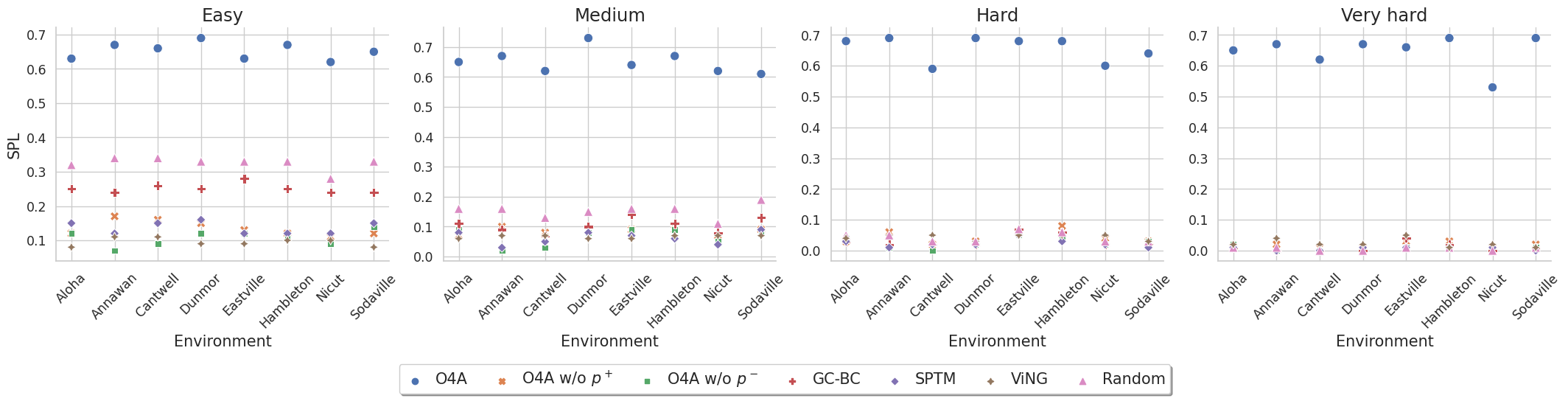
Augmentations used during Taining










Citation
@article{morin2023one,
title = {One-4-All: Neural Potential Fields for Embodied Navigation},
author = {Morin, Sacha and Saavedra-Ruiz, Miguel and Paull, Liam},
year = 2023,
journal = {arXiv preprint arXiv:2303.04011}
}


