Robotics Group @ University of Montreal | Inverse Variance Reinforcement Learning

Inverse Variance Reinforcement Learning

Most robotics problems can be written as (Partially Observable) Markov Decision Processes (MDPs), with discrete or continuous observation and action spaces. Deep Reinforcement Learning (DRL) is a powerful tool to find an optimal policy for these processes, based on experience acquired during the training process. The training of a DRL agent requires many trajectories, which can be arduous and expensive to produce in the real world. Indeed, the real world is not parallelizable, may require human efforts to reset, and comes with risks for the robot and the environment. Gathering sufficient experience is therefore one of the most important challenges when applying DRL to robotics. The objective of this project is to reduce the amount of samples necessary to train a DRL agent on a robot.

A diagram representing the generation process of the noisy target.

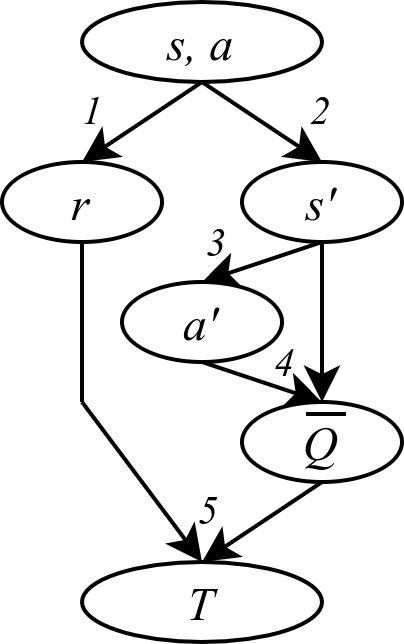
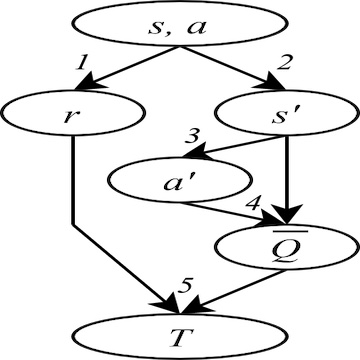
DRL algorithms are complex processes. An important part of most model-free algorithms is learning the value function of a given state or state-action pair, i.e., the expected return given the current policy. To do so, deep supervised learning components are used, where the input is the state(-action), and the label is called the target. The target T is a noisy sample of the value. Often, it is computed using the reward r and the next state s’ sampled from experience, the next action a’ based on s’ and the current policy, and the value Q of the next state-action pair which is bootstrapped from the current value estimator (this is the Temporal Difference target). The noise on the target negatively impacts the learning process: the networks learn from wrong data, which entails slower learning and instability.

The key element in this project is the fact that the noise affecting in the target, i.e. its difference from the true and unique value function, is heteroscedastic. This means that the distribution it is sampled from changes for each input and training step. Sometimes, this distribution has a very low variance: the target is close to the value. Sometimes, on the other hand, the target is subject to a lot of noise and it does not contain useful information with respect to the value. Therefore, the value estimation task in DRL is a case of heteroscedastic regression.

Projects

Batch Inverse-Variance Weighting for Deep Heteroscedastic Regression

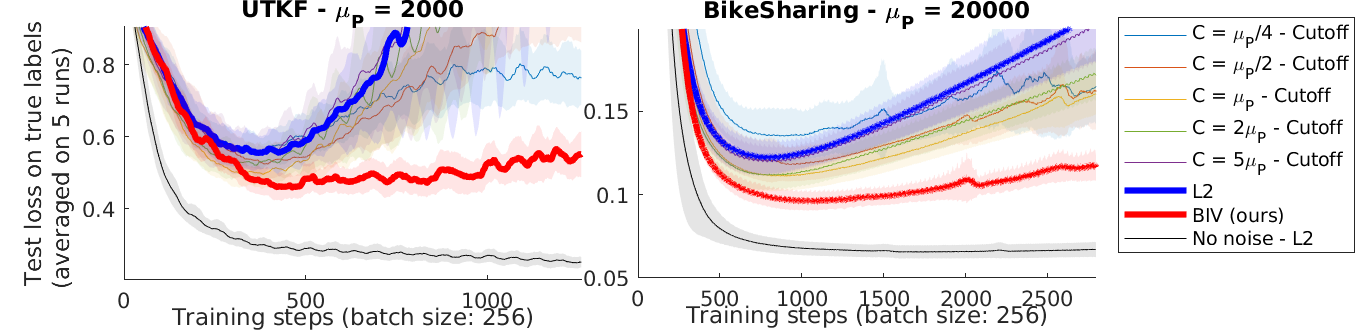
Noisy labels slows the learning process in regression: the first part of this project was to prove that the effect of noisy labels can be mitigated given the hypothesis that we know the variance of the noise distribution of each label. How can we include this additional information for heteroscedastic regression? Intuitively, we shoud give more weight to the labels we trust more. In linear regression, the Gauss-Markov theorem shows that the optimal solution is to weigh each sample by the inverse of the variance of the label noise. We show that adapting inverse-variance weighting for gradient-based optimization methods allows to significantly improve the performance of the learning process. Our paper, Batch Inverse-Variance Weighting: Deep Heteroscedastic Regression (BIV), was presented at the Uncertainty and Robustness in Deep Learning workshop at ICML 2021.

A plot showing learning curves, where BIV is doing better than L2 and some baselines. — BIV improves the learning performance with noisy labels compared to the L2 loss. Source: Batch Inverse-Variance Weighting: Deep Heteroscedastic Regression

Inverse-Variance Reinforcement Learning

See project page: https://montrealrobotics.ca/ivrl/

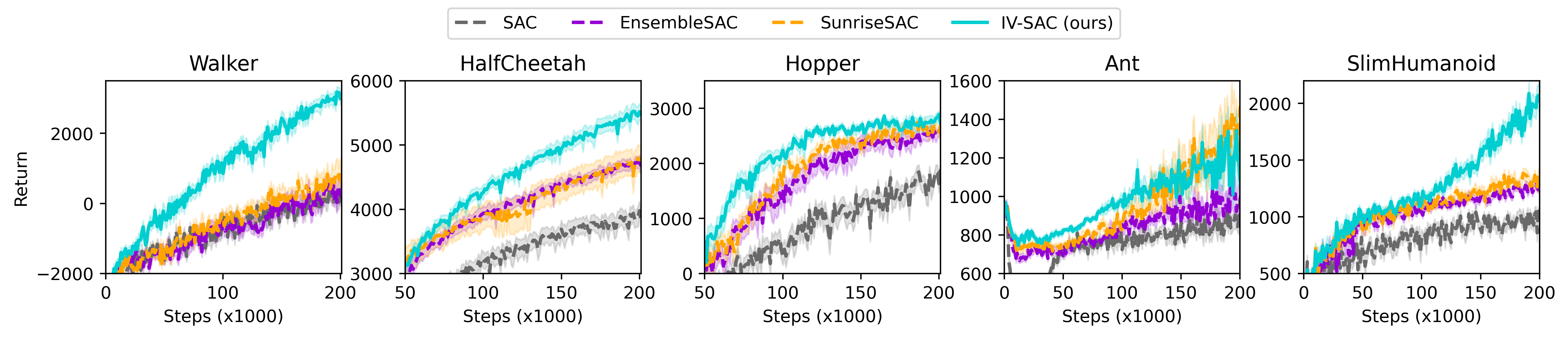
The second part of the project was to use this weighting scheme in a DRL setting. For this work, the challenge was to estimate the uncertainty of the target. A systematic analysis of the sources of uncertainty in the target generation process justifies the use of deep variance ensembles. These are used to estimate the variance due to the stochasticity of the environment and the policy, as well as the predictive uncertainty of the value prediction used to bootstrap the target. As the variance output by these deep ensembles is also the result of a training process, the uncertainty estimation is subject to complex dynamics. We show that the BIV weighting scheme is robust to changes of scale in the variance estimation. We show that combining BIV with deep variance ensembles in DRL algorithms such as DQN and SAC leads to significant improvements in the sample efficiency. This framework, called Inverse-Variance Reinforcement Learning (IV-RL), is presented in our Sample Efficient Deep Reinforcement Learning via Uncertainty Estimation submission to ICLR 2022.